भिन्न किसे कहते हैं ?
यदि किसी वस्तु के बराबर – बराबर अनेक भाग किये जाएँ, तो लिया गया प्रत्येक भाग पूरे भाग की भिन्न कहलाती है। इसे p / q के रूप में लिखते हैं। जहाँ q शून्य के बराबर नहीं होना चाहिए।
p को अंश तथा q को हर कहते हैं।
जैसे – यदि किसी तरबूज के चार टुकड़े किये जाते है जिनमे से एक टुकड़ा किसी को दे दिया जाता है तो उसे 1 / 4 के रूप में प्रदर्शित किया जाता है तथा शेष बचे हुए टुकड़े को 3 / 4 के रूप में प्रदर्शित किया जाता है।
भिन्न के उदाहरण – 1/2, 3/4, 5/6, 8/3 आदि।
भिन्न के अवयव
किसी साधारण भिन्न के दो अवयव होते हैं –
- अंश
- हर
अंश किसे कहते हैं ?
किये गए कुल भागों में से लिए गए भागों को भिन्न का अंश कहते हैं।
हर किसे कहते हैं ?
किसी वस्तु को जितने भागों में बराबर – बराबर बांटा जाता है, उसे भिन्न का हर कहते हैं।
महत्वपूर्ण नोट्स
- भिन्न में बटे के निशान (—) के ऊपर की संख्या को अंश तथा नीचे की संख्या को हर कहते हैं।
- किसी पूर्ण संख्या को उसके नीचे एक लिखकर भिन्न के रूप में व्यक्त करते हैं।
भिन्नों का चित्रमय निरूपण
जब हम किसी भिन्नात्मक भाग को किसी चित्र के द्वारा प्रदर्शित करते है। तो यह भिन्नों का चित्रमय निरूपण कहलाता है।
जैसे – 1 / 2 भिन्न को चित्र द्वारा निम्न प्रकार प्रदर्शित करते हैं –
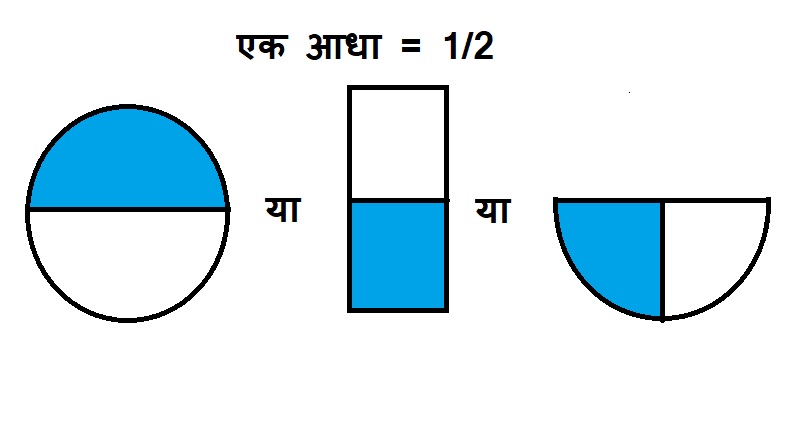
भिन्नों के चित्रमय निरूपण पर आधारित प्रश्न
4 बराबर भागों में से 3 भाग अर्थात (3 / 4) को चित्र द्वारा प्रदर्शित कीजिए।
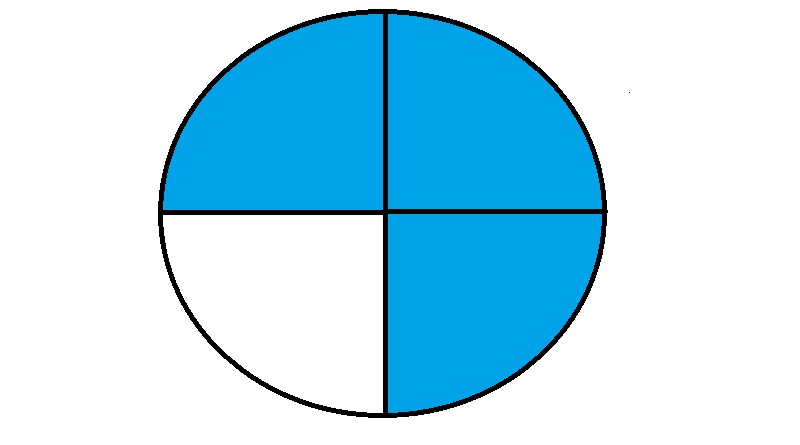
8 बराबर भागों में से 1 भाग अर्थात (1 / 8) को चित्र द्वारा प्रदर्शित कीजिए।
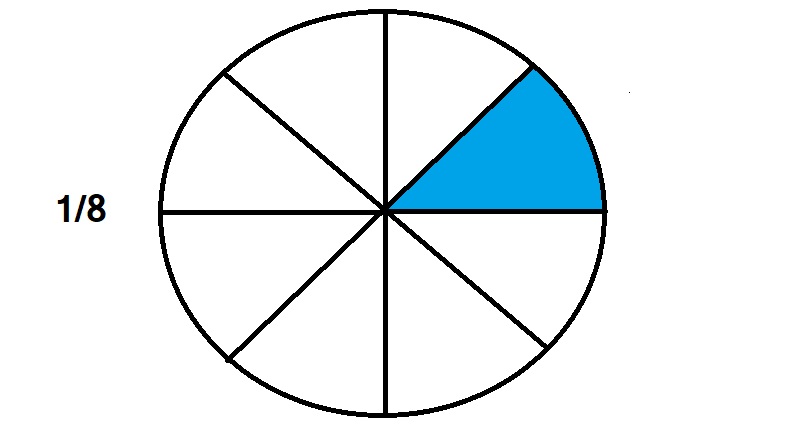
भिन्नों के प्रकार
भिन्न के निम्नलिखित प्रकार होते हैं –
- दशमलव भिन्न
- उचित भिन्न
- अनुचित भिन्न या विषम भिन्न
- संयुक्त भिन्न
- इकाई भिन्न
- व्युत्क्रम भिन्न
दशमलव भिन्न किसे कहते हैं ?
ऐसा भिन्न जिनके हर 10 या 10 के किसी भी घात के रूप में लिखे हो, दशमलव भिन्न कहलाते हैं।
जैसे – 3/10, 5/100, 7/1000 आदि।
उचित भिन्न किसे कहते हैं ?
ऐसा भिन्न जिसका अंश, हर से छोटा होता है, उसे उचित कहते है।
जैसे – 1/2, 2/5, 7/9 आदि।
अनुचित भिन्न किसे कहते हैं ?
ऐसा भिन्न जिसका अंश, हर से बड़ा होता है, उसे अनुचित भिन्न कहते हैं।
जैसे – 7/2, 5/3, 9/5 आदि।
संयुक्त भिन्न किसे कहते हैं ?
एक पूर्णाक संख्या व एक उचित भिन्न को जोड़ने पर जो योगफल मिलता है, उसे संयुक्त भिन्न कहते हैं।
जैसे – 1¾, 2¾ आदि।
इकाई भिन्न किसे कहते हैं ?
ऐसा भिन्न जिसके अंश का मान हमेशा 1 होता है, उसे इकाई भिन्न कहते हैं।
जैसे – 1/7, 1/6, 1/5 आदि।
व्युत्क्रम भिन्न किसे कहते हैं ?
यदि p/q एक भिन्न हो, तो q/p इसका व्युत्क्रम भिन्न कहलाता है।
जैसे – 6/7 एक भिन्न है तो इसका व्युत्क्रम भिन्न 7/6 होगा।
भिन्नो पर संक्रियाएँ
भिन्नों का जोड़
यदि हर समान हो,
माना दो भिन्न a/b तथा c/b हैं। जिनका हर समान है तो इनका जोड़ निम्न प्रकार होगा –
a/b + c/b = (a + c)/b होगा।
उदाहरण 1. 3/4 तथा 2/4 को जोड़िये।
हल – 3/4 + 2/4 = (3+2)/4 = 5/4
उदाहरण 2. 1/2, 3/2 तथा 5/2 को जोड़िये।
हल – 1/2 + 3/2 + 5/2
=(1+3+5)/2
= 9/2
यदि हर असमान हो,
जब भिन्नों का हर असमान होता है तो उनका योग करते समय सबसे पहले प्रत्येक भिन्न के हर का ल० स० ज्ञात करते हैं फिर प्रत्येक भिन्न के हर से ल० स० में भाग देकर प्राप्त भागफल को प्रत्येक भिन्न के अंश से गुणा कर देते हैं।
उदाहरण 1. 3/2 तथा 5/4 को जोड़िये।
हल – सबसे पहले दोनों भिन्न के हर 2 और 4 का ल० स० निकालेंगे।
2, 4 का ल० स० = 4
फिर प्रत्येक भिन्न के हर से ल० स० में भाग देकर प्राप्त भागफल को प्रत्येक भिन्न के अंश से गुणा करेंगे।
4÷2 = 2 (भागफल) x 3 = 6
4÷4 = 1 (भागफल) x 5 = 5
अतः भिन्नो का योग =
3/2 + 5/4 = (6+5)/4 = 11/4
भिन्नों का घटाव
भिन्नो का घटाव ज्ञात करने के लिए भी उपरोक्त विधि का प्रयोग करते हैं। यहाँ केवल चिन्हों का ध्यान देना होता है।
भिन्नों का गुणा
a/b x c/d = ac/bd
उदाहरण 2/3 x 4/3 को हल कीजिये।
हल = 2/3 x 4/3 = 8/9
भिन्नों का भाग
a/b ÷ c/d = a/b x d/c
उदाहरण 3/5 ÷ 1/3 को हल कीजिये।
हल = 3/5 ÷ 1/3
= 3/5 x 3/1
= 9/5
समतुल्य भिन्न किसे कहते हैं ?
किसी भिन्न के अंश तथा हर को समान संख्या से गुणा या भाग करने पर प्राप्त हुई नई भिन्न को दी गई भिन्न का समतुल्य भिन्न कहते हैं।
जैसे – 2/3 का समतुल्य भिन्न = 4/6, 6/9, 8/12, 10/15 आदि होगा।
समतुल्य भिन्न कैसे ज्ञात करते हैं ?
समतुल्य भिन्न निम्न दो तरीकों से ज्ञात करते हैं जो नीचे दिए गए हैं –
तरीका -1. किसी भिन्न के अंश और हर प्रत्येक को एक ही संख्या से गुणा करके समतुल्य भिन्न ज्ञात करते हैं।
जैसे – 2/3 का समतुल्य भिन्न ज्ञात करने के लिए उसके अंश और हर प्रत्येक को एक ही संख्या 2, 3, 4, 5 आदि से गुणा करते हैं।
2/3 का समतुल्य भिन्न = 4/6, 6/9, 8/12, 10/15 आदि।
तरीका -2. किसी भिन्न के अंश और हर प्रत्येक को एक समान संख्या (2, 3, 4, 6) से भाग देकर समतुल्य भिन्न प्राप्त करते हैं।
जैसे – 24/120 का समतुल्य भिन्न = 12/60, 8/40, 6/30, 4/20 आदि।
इसे भी पढ़ें –
Number System( संख्या पद्धति ) – Concept, Formulas, Questions And Tricks
स्थानीय मान एवं जातीय मान बारीकी से समझें
वृत्त की परिभाषा, सूत्र एवं वृत्त के गुण
त्रिभुज किसे कहते हैं त्रिभुज के प्रकार एवं सूत्र
चतुर्भुज किसे कहते हैं ? चतुर्भुज के प्रकार

